IL METODO ALGEBRICO
Il N. A. ha le sue definizioni di "divisione" e di "sezione", poiché è l'unico numero che soddisfa il seguente problema:
Dato un segmento x + y, dividerlo in due segmenti x ed y tali che il rapporto che c'è tra il più piccolo ed il più grande sia uguale al rapporto tra il più grande e la somma dei due. In termini matematici il tutto si traduce cos�:
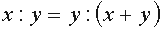
chiamando x il segmento più corto e y quello più lungo.
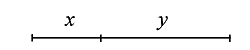
Come unità di misura può essere adottato sia il segmento x che x + y. Si possono cioè impostare due proporzioni diverse: una che considera x = 1, e l'altra che considera x + y = 1.
Sia esaminando entrambi i casi, dopo alcuni passaggi si giunge comunque ad un'equazione di secondo grado. Si prenda ad esempio l'equazione risultante dal primo caso, in cui la variabile x è scomparsa. L'equazione risulta:
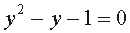
Come tutte le equazioni di secondo grado, anche qui si hanno due radici reali e distinte: una è -1,2360679775..., mentre l'altra è 1,61803398875..., che è il N. A. propriamente detto.
Durante i passaggi intermedi, ad un certo punto si giunge all'equazione:
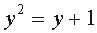
il N. A., infatti, elevato al quadrato è:
1,618033988752 = 2,61803398875...
Come si può vedere, è l'unico numero decimale il cui quadrato è uguale al numero stesso aumentato di una unità.
Tra l'altro, anche il numero che è stato trovato dall'equazione seguendo l'altro procedimento fa parte della sezione aurea, anche se non è propriamente il N. A.. Esso si ottiene ponendo uguale a 1 la somma dei segmenti, che risultano rispettivamente lunghi 0,382... e 0,618... Anche questi due valori hanno proprietà interessanti.
Ad ogni modo, la "vera" sezione aurea, quella, cioè più comunemente usata, è quella incontrata prima.
IL METODO ARITMETICO
Il matematico FIBONACCI (che lavorava, peraltro, nella corte di FEDERICO II) è noto soprattutto per la sua famosa serie, che da lui prende il nome.
Questa serie è formata da numeri tali che ognuno di essi è la somma dei due precedenti:
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 - 89 - 144 ...
Calcolando il rapporto fra ciascun numero della serie ed il suo precedente, si ottengono risultati che oscillano intorno al N. A., con un'approssimazione sempre maggiore.
Infatti:
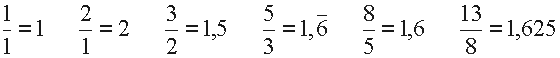 ...
...
Continuando a calcolare altri numeri della serie ed altri rapporti, si raggiungono risultati sempre più vicini al N. A., con un numero di decimali sempre più grande.
IL NUMERO AUREO NELLA GEOMETRIA
I rettangoli aurei
Il pentagono ed il pentacolo
| D | C | |
 | ||
| A | B |
Un rettangolo è detto "aureo" quando uno dei lati (es. la base) è uguale al doppio dell'altro. La diagonale risulta, calcolata con il teorema di Pitagora, pari alla radice quadrata di 5:
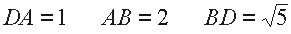
Il segmento ottenuto sommando la diagonale all'altezza, se diviso per la base, d� il valore esatto del Numero Aureo. Cioè:
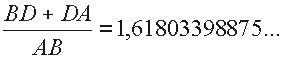
Dato che la figura ABD è un triangolo rettangolo, il procedimento può essere esteso anche a questo tipo di poligoni.
Tra l'altro, l'area di un triangolo rettangolo che ha un cateto pari a 1 e l'altro pari a radice di 5, è 1,61803398875...
A proposito dei triangoli rettangoli, è stato citato PITAGORA, fondatore di una scuola filosofica che poneva i numeri alla base del creato. A lui è attribuita una frase, secondo la quale il pentacolo, o stella a cinque punte, rappresenta perfettamente il N. A..
Volendo scoprire il motivo di tale affermazione, si può provare ad analizzare la figura, che può essere facilmente disegnata senza staccare la penna dal foglio.
Se lo si analizza, ci si accorge che la figura è formata da un pentagono centrale, con un triangolo isoscele disposto su ciascun lato. In ciascuno dei triangoli, il rapporto fra uno dei lati maggiori e il lato più piccolo (e quindi il lato del pentagono) è ancora una volta 1,61803398875...
Questo rapporto, tra l'altro, è anche il rapporto che c'è tra la diagonale di un pentagono ed il suo lato.